Scattering Functions S(α, β): An Examination of Elastic and Inelastic Behavior in Neutron-Matter Interactions

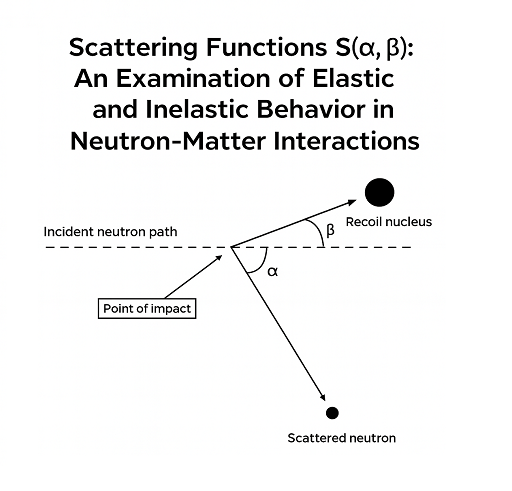
The scattering function S(α, β) is a fundamental physical quantity in the study of neutron interactions with matter. This function describes the probability of energy and momentum transfer between the neutron and the target system. The behavior of this function is divided into two distinct categories: elastic and inelastic. In elastic scattering, the internal energy of the target system does not change, and energy exchange is solely related to the motion of the center of mass. In contrast, inelastic scattering causes internal excitation of the system (such as lattice vibrations or electronic excitations). This article elaborates on the mathematical description, physical characteristics, and governing conditions for each of these states and demonstrates their importance in nuclear reactor simulations and materials science.

 

Introduction

When a neutron interacts with matter, it can transfer part of its energy and momentum to the target atoms. The nature of this transfer reveals the physical properties of the material. The double differential scattering cross section, denoted by S(α, β), is the core of this statistical description. This function depends on two dimensionless parameters:

• α (momentum parameter): Represents the reduced momentum transfer.
• β (energy parameter): Represents the reduced energy transfer.

The mathematical definition of these parameters is as follows:

​  

  ​

Where:

• ℏ  is the reduced Planck constant.
• q  is the momentum transfer vector.
• ω  is the angular frequency of the energy transfer.
• M  is the mass of the target atom.
• kB ​ is the Boltzmann constant.
• T  is the system temperature.

S(α, β) is essentially the space-time Fourier transform of the atomic pair correlation function and provides complete information about the atomic dynamics of the material.

2. Elastic Scattering S(α, β)

2.1. Physical Concept

In ideal elastic scattering, no energy is transferred to the internal degrees of freedom of the system (such as phonon vibrations). All transferred energy is used for the recoil motion of the target atom's center of mass. This occurs mainly at very low temperatures or when the neutron energy is too low to excite the lattice.

2.2. Mathematical Characteristics

In purely elastic scattering, a strict relationship exists between energy transfer and momentum transfer (the recoil energy of a free atom). This relationship is given by:

Comparing this with the definitions of α and β, we arrive at the simple relation:

 

where  ​ is the ratio of the target atom mass to the neutron mass.

Consequently, the S function for elastic scattering is non-zero only along this line in the α-β plane. Therefore, it can be expressed as a Dirac delta function:

where f(α) is a function describing the details of the static structure of the material (such as scattering from a stationary lattice). In crystalline solids, this part leads to the appearance of Bragg peaks.

3. Inelastic Scattering S(α, β)

3.1. Physical Concept

In the real world, especially at elevated temperatures, inelastic scattering is dominant. In this process, the neutron can:

• Create a phonon (lose energy: β > 0).
• Absorb a phonon (gain energy: β < 0).
• Create other excitations, such as electronic or magnetic excitations.

These excitations mean there is no fixed relationship between α and β, and the S(α, β) function spreads over a continuous region in the α-β plane.

3.2. Mathematical Characteristics

The inelastic function has important properties:

1. Principle of Detailed Balance: This physical principle states that the probability of a process and its inverse are related by a Boltzmann factor:

This relation ensures the system ultimately reaches thermal equilibrium.

2. Normalization: The integral of the S function over all β must yield a static structure function:

where  S(α) is the static structure function.

3. Broadening: Unlike the sharp elastic peak, the inelastic function is a continuous, broad distribution whose shape is directly related to the material's vibrational density of states (phonon spectrum). Modeling often uses approximations like the Gas Model or the incoherent harmonic approximation to compute S(α, β).

4. Comparison and Applications

Feature	Elastic Scattering	Inelastic Scattering
Energy Transfer	Only to center-of-mass motion	To internal degrees of freedom (phonons, etc.)
Relationship between α and β	(straight line)	No deterministic relationship
Shape of S(α, β)	Delta function along a line	Continuous distribution over a region
Dependence on Temperature	Weak (mainly through the Debye-Waller factor)	Very strong (directly dependent on the density of excited states)
Primary Application	Determining crystalline structure (neutron diffraction)	Studying atomic dynamics (neutron spectroscopy)

Practical Applications:

• Nuclear Reactor Design: Accurate calculation of neutron thermalization (slowing down of fast neutrons by inelastic collisions with moderators like water or graphite) depends entirely on the inelastic S(α, β) functions. Data libraries like ENDF/B contain computed S(α, β) values for various materials.
• Neutron Spectroscopy: By measuring the double differential scattering cross section, S(α, β) can be extracted, providing information about the phonon spectrum and material dynamics.

5. Conclusion

Scattering functions S(α, β) are powerful tools for the microscopic description of neutron-matter interactions. The distinction between elastic and inelastic states is of fundamental importance. Elastic scattering, where internal energy remains unchanged, is used to study the static structure of materials. In contrast, inelastic scattering, which involves changes in internal energy, opens a window into the dynamic world of atomic vibrations and energy transfer processes. A full understanding of these functions is essential for advancing technologies such as nuclear energy and advanced materials science.

6. Modeling S(α, β) Functions in the MCNP Code

6.1. Introduction to MCNP

MCNP (Monte Carlo N-Particle) is a widely used simulation code for neutron, photon, and electron transport, developed by Los Alamos National Laboratory. It uses the Monte Carlo method to accurately compute particle interactions.

6.2. Importance of Modeling S(α, β) in MCNP

For accurate simulation of thermal neutron behavior (energies below 1-2 eV) in moderator materials (like water, paraffin, graphite), simplified cross-sections are insufficient. In this energy range, neutron interaction depends heavily on the atomic dynamics of the target material and can only be correctly described using S(α, β) functions. MCNP uses data libraries containing S(α, β) tables for various materials.

6.3. Implementation in MCNP

a) Data Libraries:

MCNP uses nuclear data libraries like ENDF/B (Evaluated Nuclear Data File) by default. For important thermal materials (e.g., H in H₂O, D in D₂O, graphite, beryllium), these libraries contain tables of S(α, β) values over a wide range of α and β parameters and at different temperatures.

b) MCNP Input Commands:

To activate thermal calculations, the user must define specific cards in the MCNP input deck:

·         M Card: This card defines material cross-sections. For thermal materials, a special suffix called "ter" (for thermal) is added. For example:

 

M1 1001.70ter 2   # Material 1: Hydrogen (Z=1, A=1) using thermal data (S(α,β))

The 70ter suffix instructs MCNP to use thermal library data (including S(α, β)) for hydrogen instead of a simple cross-section.

·         TM Card: This card sets the temperature of the material (in MeV). Since S(α, β) is highly temperature-dependent, this card is crucial.

text

TM1 2.53e-8  # Sets temperature of Material 1 to 293.6K (room temperature).

This temperature must match the temperature for which the S(α, β) data were evaluated.

c) Simulation Process:

When a thermal neutron collides with an atom in the target material, MCNP performs the following steps:

1. It has the neutron's collision energy and angle.
2. Based on the defined material and temperature, it consults the S(α, β) table.
3. Using Monte Carlo sampling methods, it selects specific values for energy transfer (β) and momentum transfer (α) from the probability distribution defined by S(α, β).
4. It updates the neutron's energy and direction after scattering.
5. This process is repeated for millions of particles and collisions to obtain a valid statistical result.

6.4. Materials Modelable with S(α, β) in MCNP

Common materials for which S(α, β) data is available in MCNP include:

• Hydrogen (in water H₂O, ice, paraffin, polyethylene)
• Deuterium (in heavy water D₂O)
• Beryllium (Be)
• Graphite (C)
• Oxygen (O in H₂O)
• Other important moderator materials.

For other materials, MCNP uses simpler models like the Free Gas Model as an approximation.

6.5. A Simple MCNP Input Example

A very simple example of defining a thermal material in MCNP is shown below:

Example Input Deck for Thermal Neutron Scattering
C Cell Cards
1 1 -1.0 -10   $ Cell filled with water (density 1.0 g/cm³) inside surface 10
2 0 10         $ External cell (vacuum)

 
C Surface Cards
10 SO 10       $ Sphere with a radius of 10 cm

C Data Cards
M1 1001.70ter 2 8016.70ter 1  $ Material 1: Water (H-1 and O-16 with thermal data)
TM1 2.53e-8   $ Water temperature = 293.6K
MODE N        Neutron transport only
NPS 100000    Run 100,000 particle histories
SDef POS=0 0 0 ERG=0.025eV  $ Thermal neutron source at center with energy 0.025 eV
F4:N 10       Tally neutron flux in cell 10

6.6. Advantages and Limitations
Advantages:

• High Accuracy: Provides a realistic simulation of thermal neutron scattering.
• Temperature Dependence: Correctly accounts for the effect of temperature on the thermalization process.
• Industry Standard: A validated and accepted method for reactor and shielding calculations.

Limitations:

• Complexity: Producing accurate S(α, β) data for new materials is very complex and requires neutron scattering experiments.
• Computational Resources: Thermal calculations are typically more resource-intensive and time-consuming than calculations with simple cross-sections.

7. Final Conclusion

Scattering functions S(α, β) are the bridge between the microscopic dynamics of materials and the macroscopic behavior of neutrons. Distinguishing between elastic and inelastic states is essential for understanding energy and momentum transfer. Powerful codes like MCNP, by implementing these functions in the form of library data and Monte Carlo sampling algorithms, enable accurate simulation of complex nuclear systems such as reactors, imaging systems, and medical devices. The success of such simulations depends directly on the accuracy of the S(α, β) data, underscoring the importance of basic research in the field of thermal neutron scattering.

Supplementary Resources for the MCNP Section:

 

• MCNP User's Manual, Code Version 6.2, Los Alamos National Laboratory.
• ENDF/B-VIII.0 Library, National Nuclear Data Center, Brookhaven National Laboratory.
• M. B. Chadwick et al., "ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data," Nuclear Data Sheets, 2018.